Můžete přemýšlet, jaký je dnes obyčejný den. Půjde o obvyklý otisk do plochy života, kterou postupně pokrýváte. Mimochodem, pokrytí plochy dlaždicemi jednoho nebo více tvarů, aniž by se překrývaly, je pěkná matematická úloha (tiling). Pokud jste "Ryba", mohla by plocha života vypadat jako následující obrázek pokrytý pětiúhelníky (Ryby od Majorie Rice).




Můžete přemýšlet, že dnešek jako obyčejně nebude perfektní. Jak jdete životem, hrany "víceúhelníků" přibývají i ubývají. Mimochodem, matematika plochu pokrývá spíše perfektními tvary, kdežto člověku se občas přihodí drobná vada. To věděli i lidé v Novém Mexiku před tisícem let, když zdobili džbánky. Když se zadíváte na džbánek z následujícího obrázku, pozorujete, že zubatá bílá linka vlevo má tři zuby, zatímco vpravo čtyři. Dva odlišné vzory? Nebuďte přísní. Umělecké vyjádření jednoho vzoru.



Můžete přemýšlet, že jako obyčejně začnete pracovat. Třeba řešit prostou kvadratickou rovnici x^2-x-1=0. Mimochodem, kladným řešením rovnice je 1.618... Délkově určuje tzv. zlatý řez, což je poměr délek 1:1.618... Ten působí esteticky lahodným dojmem, jak můžete obdivovat na následujícím obrázku.



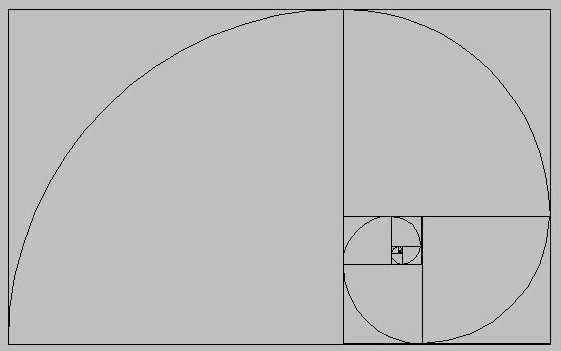
Můžete přemýšlet, co ta obyčejná křivka ovládaná zlatým řezem připomíná. Třeba prohlédnout příručku živočišných nebo rostlinných druhů. Mimochodem, právě jste vyšli z obyčejnosti. Udělali objev. Jak matematicky popsat tvar části přírody. Třeba takový, jaký je na následujícím obrázku. Tak Vám přeji hodně východů z obyčejnosti.



P.S. Je velmi hezké být obyčejným a neperfektním bloggerem.

Zdroj obrázků: For All Practical Purposes: Introduction to Contemporary Mathematics. Fourth edition. W.H. Freeman and Company, 1997