V plochosti
Plochost nebo pád do plochosti obyčejně znamenají něco nezajímavého. Může tomu být naopak.
Nedlouho před prvním miléniem došlo k výraznému postupu v algebře. Někdy kolem roku 820 byla například známa kladná celočíselná řešení několika typů kvadratických rovnic.
Jednou z nich byla rovnice X2+12X=45. Na levou stranu se pohlíželo jako na spojení dvou ploch: plochy čtverce X2, jehož strana je X a plochy obdélníka, jehož délka je 12 a výška X. Výzvou tehdy byla otázka, jak lze uvedené dvě plochy představit jako čtverec o ploše 45. Prosté spojení ploch čtverce a obdélníka na levé straně ke čtverci nevedlo.
Došli k představě (pravděpodobně studiem Eukleidových Základů), že obdélník s plochou 12X spojuje dva obdélníky se stranami 6 a X. Kombinací čtverce se stranou X s uvedenými obdélníky vznikne "vykousnutý" čtverec se stranou X+6. Jeho doplnění o plochu 6x6 vytvoří úplný čtverec o ploše 45+36=81.
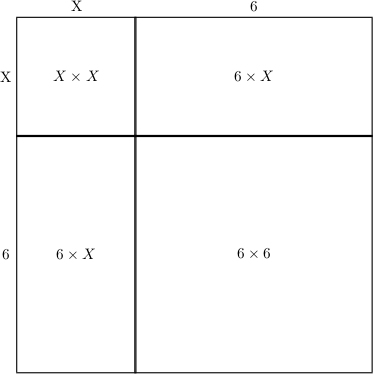
Platí tedy, že (X+6)2=81. Vzhledem ke čtverci 9x9=81 je X+6=9 a nakonec X=3. Vystačila plochost na řešení kvadratických rovnic? Problém by vyvstal hned při změně o "pouhou" 1 na pravé straně na X2+12X=46. V tu chvíli by řešení vyžadovalo odmocninu z 82, tedy iracionální číslo.
Řešení znamenalo výrazný postup, i když zdaleka nezahrnovalo všechny kvadratické rovnice. Přemýšlím, jak vůbec může v plochosti existovat výrazný postup. Nemám pochybnost, že lidský život podobně jako západní společnost jsou v určitém smyslu ploché podobně jako uvedené řešení kvadratických rovnic pomocí ploch. Matematice trvalo dalších takřka tisíc let, než přijala iracionální čísla. V uvedené plochosti se objevují tři veličiny, které mohou za výrazným postupem stát: inspirace význačným dílem, proveditelnost a vysoký grit (zaměřenost na dlouhodobé cíle). Jejich působení může vést k přitažlivé plochosti. A tu mi prosím dovolte popřát.
Nedlouho před prvním miléniem došlo k výraznému postupu v algebře. Někdy kolem roku 820 byla například známa kladná celočíselná řešení několika typů kvadratických rovnic.
Jednou z nich byla rovnice X2+12X=45. Na levou stranu se pohlíželo jako na spojení dvou ploch: plochy čtverce X2, jehož strana je X a plochy obdélníka, jehož délka je 12 a výška X. Výzvou tehdy byla otázka, jak lze uvedené dvě plochy představit jako čtverec o ploše 45. Prosté spojení ploch čtverce a obdélníka na levé straně ke čtverci nevedlo.
Došli k představě (pravděpodobně studiem Eukleidových Základů), že obdélník s plochou 12X spojuje dva obdélníky se stranami 6 a X. Kombinací čtverce se stranou X s uvedenými obdélníky vznikne "vykousnutý" čtverec se stranou X+6. Jeho doplnění o plochu 6x6 vytvoří úplný čtverec o ploše 45+36=81.

Platí tedy, že (X+6)2=81. Vzhledem ke čtverci 9x9=81 je X+6=9 a nakonec X=3. Vystačila plochost na řešení kvadratických rovnic? Problém by vyvstal hned při změně o "pouhou" 1 na pravé straně na X2+12X=46. V tu chvíli by řešení vyžadovalo odmocninu z 82, tedy iracionální číslo.
Řešení znamenalo výrazný postup, i když zdaleka nezahrnovalo všechny kvadratické rovnice. Přemýšlím, jak vůbec může v plochosti existovat výrazný postup. Nemám pochybnost, že lidský život podobně jako západní společnost jsou v určitém smyslu ploché podobně jako uvedené řešení kvadratických rovnic pomocí ploch. Matematice trvalo dalších takřka tisíc let, než přijala iracionální čísla. V uvedené plochosti se objevují tři veličiny, které mohou za výrazným postupem stát: inspirace význačným dílem, proveditelnost a vysoký grit (zaměřenost na dlouhodobé cíle). Jejich působení může vést k přitažlivé plochosti. A tu mi prosím dovolte popřát.

 Deník dobrovolníka: Vítej, český bratře! Ukrajinci děkovali za pomoc na každém kroku
Deník dobrovolníka: Vítej, český bratře! Ukrajinci děkovali za pomoc na každém kroku Laskavý duchovní i tvrdý politik. Františkův pontifikát se uzavřel bez revoluce
Laskavý duchovní i tvrdý politik. Františkův pontifikát se uzavřel bez revoluce Konečně! Trumpův mírový plán pro Ukrajinu je zde
Konečně! Trumpův mírový plán pro Ukrajinu je zde Anglický deník: Krysí kalamita? Místní si o to koledovali
Anglický deník: Krysí kalamita? Místní si o to koledovali Odešel renesanční psychiatr Cyril Höschl
Odešel renesanční psychiatr Cyril Höschl

