Prameny počáteční matematiky
Prameny zahrnují nevelké území rozsahu jedné bouře. Viz přiložený obrázek.
Rhindův papyrus obsahuje mimo jiné příklady pro kvadratické rovnice. Na hliněné tabulce Plimpton 322 je seznam pythagorejských trojic, tedy opět kvadratických rovností.
Prameny staroegyptské geometrie a babylonské aritmetiky mířily do starověkého Řecka, kde 800 let zesilovaly v řeku. Odtud se řeka přelila do Arabské říše a Indie, aby ji ve vrcholícím středověku a počátku novověku Evropa změnila na veletok. Za vůbec největší matematiky bývaji označováni v pořadí Archimedes a I. Newton.
Matematice podle všeho nejvíce prospívají kvetoucí obchod, řemesla a chrámy. Za zmínku také stojí, že matematický veletok vznikl bez moderních prvků jakými jsou projekty nebo granty.
Už starověcí matematici a nejvíce patrně Archimedes považovali Vesmír za matematický. To je pozoruhodné zvlášť ve spojení s obchodem, řemesly a chrámy. Že Vesmír má své kvetoucí chrámy už známe. Obchod, tedy nabídku-poptávku může představovat gravitace, která ve Vesmíru jenom kvete. Kvetoucími řemesly potom mohou být chemické prvky a jejich souhra nebo dokonce život.
Matematika proto učí pozorovat pravdu. Tím se řadí spíše mezi ctnosti. Z pohledu, že ctnost má dvě části, pozorování pravdy a jak jednat, jde o polovinu ctnosti. I ta je nezanedbatelná. Další neméně pozoruhodná věc spočívá ve vyčerpání místa po nějakém čase a čeká to patrně i Evropu a také ve faktu, že některé i početné společnosti matematiku rozvíjet nepotřebovaly.
Je proto namístě v čase, kdy jsou louky díky květům nejhezčí, aby stejně kvetly obchod, řemesla a chrámy. Tedy něco, co je blízké matematickému Vesmíru. A to mi prosím dovolte popřát. Vypravit se o víkendu na některý z mostů přes matematický veletok.
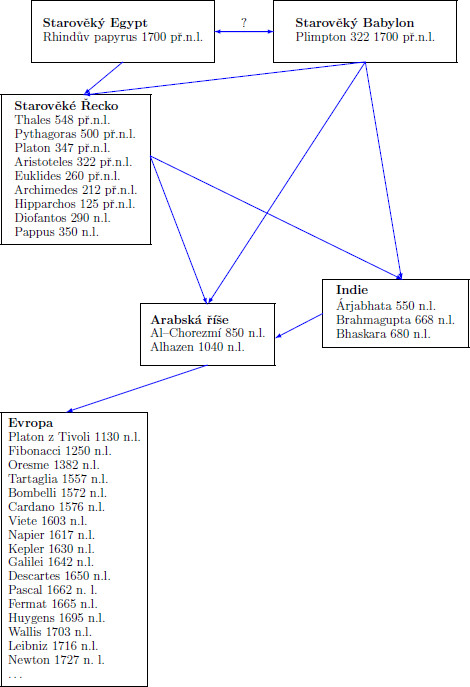
Rhindův papyrus obsahuje mimo jiné příklady pro kvadratické rovnice. Na hliněné tabulce Plimpton 322 je seznam pythagorejských trojic, tedy opět kvadratických rovností.
Prameny staroegyptské geometrie a babylonské aritmetiky mířily do starověkého Řecka, kde 800 let zesilovaly v řeku. Odtud se řeka přelila do Arabské říše a Indie, aby ji ve vrcholícím středověku a počátku novověku Evropa změnila na veletok. Za vůbec největší matematiky bývaji označováni v pořadí Archimedes a I. Newton.
Matematice podle všeho nejvíce prospívají kvetoucí obchod, řemesla a chrámy. Za zmínku také stojí, že matematický veletok vznikl bez moderních prvků jakými jsou projekty nebo granty.
Už starověcí matematici a nejvíce patrně Archimedes považovali Vesmír za matematický. To je pozoruhodné zvlášť ve spojení s obchodem, řemesly a chrámy. Že Vesmír má své kvetoucí chrámy už známe. Obchod, tedy nabídku-poptávku může představovat gravitace, která ve Vesmíru jenom kvete. Kvetoucími řemesly potom mohou být chemické prvky a jejich souhra nebo dokonce život.
Matematika proto učí pozorovat pravdu. Tím se řadí spíše mezi ctnosti. Z pohledu, že ctnost má dvě části, pozorování pravdy a jak jednat, jde o polovinu ctnosti. I ta je nezanedbatelná. Další neméně pozoruhodná věc spočívá ve vyčerpání místa po nějakém čase a čeká to patrně i Evropu a také ve faktu, že některé i početné společnosti matematiku rozvíjet nepotřebovaly.
Je proto namístě v čase, kdy jsou louky díky květům nejhezčí, aby stejně kvetly obchod, řemesla a chrámy. Tedy něco, co je blízké matematickému Vesmíru. A to mi prosím dovolte popřát. Vypravit se o víkendu na některý z mostů přes matematický veletok.


 Fiala v ohrožení. Premiér místo vysvětlování raději otvíral sokolovnu u Brna
Fiala v ohrožení. Premiér místo vysvětlování raději otvíral sokolovnu u Brna Babiš lechtá mladé na bradě. AB merchem rozjel fenomén, který nejde zastavit
Babiš lechtá mladé na bradě. AB merchem rozjel fenomén, který nejde zastavit Akce Zámky Přemysla Pittra pomohla po válce dětem s návratem do života
Akce Zámky Přemysla Pittra pomohla po válce dětem s návratem do života Přežijí novináři autokraty?
Přežijí novináři autokraty? Varšava dokáže být ve vztahu k Moskvě racionální. I přes historickou zkušenost
Varšava dokáže být ve vztahu k Moskvě racionální. I přes historickou zkušenost

