Kdo nezná teorii her, je to disciplína aplikované matematiky, která analyzuje různé konfliktní situace, ve které dochází ke střetu zájmů. Herně-teoretické modely se snaží tyto konfliktní situace analyzovat a s pomocí matematického modelu vypočítat nejlepší scénáře pro konkrétní účastníky konfliktu.
Analogicky definujme celý kapitálový trh jako hru s nulovým součtem, nebo-li pokud jeden účastník na trhu vydělá, jde jeho výdělek na úkor jiného účastníka na trhu. Je možné využít teorii her v náš prospěch z pohledu investora-účastníka na trhu? Čtěte dále...


Jedním z užitečných modelů v teorii her se nazývá Parrondův Paradox. Parrondův Paradox byl v teorii her popsán jako kombinace prohrávajicích strategií, která se v konečném důsledku stává vítěznou strategií, kde strategií nazýváme investici (akciový fond, fond privátního kapitálu atd.). Paradox byl pojmenován po tvůrci Juanu Parrondovi, který tento paradox objevil v roce 1996. Popisuje jí následovně: existuje-li dvojice her, každá s vyšší pravděpodobností ztráty než vítězství, pak je možné sestavit vítěznou strategii tím, že hraje hry střídavě.

No není to kacířská myšlenka? Jak je vůbec možné, aby bylo možné teoreticky vydělávat na ztrátových investicích? A tím nemyslím vydělávat ve smyslu prodávat “zaručený způsob jak vydělat investováním" nekvalifikovaným investorům. Naneštěstí pro milovníky hazardních her, Parrdondův paradox nebude fungovat u hazardních her a kasína.

Někdě musí být háček. Zkusme se na problematiku podívat matematicky. Jak tedy zní definice Parrondova paradoxu? Představme si 2 nekorelované ztrátové investice A a B. První je jednoduchá a druhá je komplexní. Jednoduchá investice A je charakteristická tím, že za každý týden zaznamená zisk ve výši 1$ s pravděpodobností P a následovně s pravděpodobností 1-P naopak zaznamená ztrátu ve výši 1$. Komplexní investice B je sama o sobě kombinací dvou jednoduchých investic, řekněme B1 a B2, z nichž každá je stejně jednoduchá jako investice A.

V investici B1 je pravděpodobnost týdenního zisku 1$ P1, zatímco v investici B2 je pravděpodobnost zisku P2. Dále existuje pravidlo, že v investici B je investice B1 investována, pokud celkový kapitál portfolia investic A a B dosahuje n-násobku proměnné M, kde M>1. Pokud je M<1, pak je investována investice B2. Investice A a B může být zkombinována mnoha způsoby. Kombinace může být tvořena náhodně s předem danou pravděpodobností výběru investice A. Nebo je kombinace sekvencí investic se vzorkováním AABB. Nebo-li dva týdny obchodujeme s investicí A a za další dva týdny obchodujeme s investicí B. Kapitál přesouváme mezi investicemi jak je třeba.

A tady přichází zlom. Aby platila definice paradoxu, všechny tři investice dohromady, tj. A, B1 a B2 nesmějí být ztrátové. Pro M = 2 nebo max 3 vychází B stále jako ztrátová investice, niceméně se stává ziskovou pro M>3. Pro ilustraci si zkusme vygenerovat 500 iterací po 100 týdenních obchodovacích periodách, kde tři investice A, B1 a B2 mají pravděpodobnostní rozdělení P = 0.5, P1 = 0.1, P2 = 0.75. Investice B2 vychází jako nejziskovější a je “chytřejší” než trh o 25%.



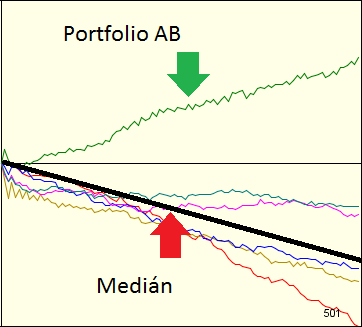
Jak je vidět z obrázku, díky paradoxu je kombinace ztrátových investic zisková. Je třeba upozornit na to, že zelená křivka představuje sekvenci ABBAB, tudíž v sekvenci převažuje investice B, v které je podinvestice B2 jako jedinná zisková. A tady narážíme na jádro problému. V kombinaci investic musí existovat alespoň jedna investice, jejíž pravděpodobnost ziskovosti převažuje zbylé investice a navíc každá z investic splňuje definice popsané výše. Díky simulaci jsme si dokázali, že není všechno zlato co se třpytí a z fundamentálně špatné investice se nemůže stát zisková. Možná by k tomuto závěru postačil selský rozum, ale je zajímavější popsat jednoduchou problematiku rigorozním způsobem.

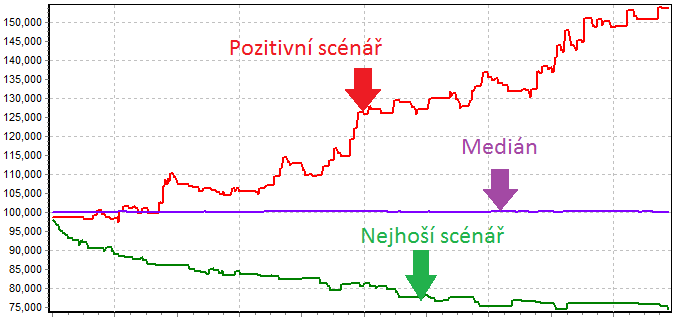
Dosud jsme se patlali v definicích, teorii a konečně i v simulaci. Jak by ale vypadala aplikace paradoxu v praxi? Pro tyto účely jsem vytvořil 2 ztrátové strategie a jednu “mírně ziskovou”, která má matematické očekávání lehce nad nulou. Je nutno dodat, že žádná strategie nemá procento výher nižší než 30% a všechny mají pozitivní poměr výher ku proher. Následně jsem provedl složení portfolia a přes Monte Carlo simulaci vytvořil 10 000000 iterací potenciálních scénářů. Jak je z obr. níže vidět, nejhorší scénář bude vždy ztrátový. Medián se drží nad nulou díky vyšší váze ziskové strategie, avšak co nás zajímá nejvíce je konečný efekt paradoxu na reálné portfolio. A ten se dostavil ve formě jedné z mnoha pozitivních scénářů, kdy křivka portfolia směle stoupá vzhůru a během 500 obchodovacích cyklů dosáhl výnosu 52%. Pokud Vás problematika zajímá více, zanechte komentář a nashledanou u dalšího článku.