S trochou nadsázky lze říci, že jsou dvě pravidla hledání pravdy. První pravidlo je mít stroj nebo lidskou inteligenci. Druhé pravidlo je štěstí na dobrý úsudek. Přitom odoláváme stavu, že jednoduché pravdy nemohou být nepravdivé.

Pravdu obvykle vyjadřujeme slovesem "je" nebo znakem =. Například "nebe je modré" nebo 1+2+3+4=10. Matematika používá úplné důkazy. Tedy postupy, které zpravidla začínají dobrou myšlenkou a končí ověřením pravdivosti bez jakékoli nejistoty. Například Pythagorova věta platí v dané geometrii bez jakýchkoli pochybností.

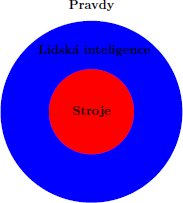
Úplné důkazy jsou v běžném životě zřídkavé. A to i v takových vědách, jako jsou fyzika nebo právo. Z matematiky v této souvislosti vychází význačný výsledek. Zjednodušeně řečeno říká, že nelze naprogramovat stroj, který by našel veškeré pravdy. Pokaždé tu zůstane prostor pro lidskou inteligenci, jak ilustruje obrázek. Ta může vidět věci dalším způsobem, něco dodat, vyprávět příběhy jinak apod.


Matematika proto představuje málo dostižný terén. Z pohledu úplných důkazů něco jako hlubokomořský Mariánský příkop. V běžném životě by proto dávalo smysl stupně pravdivosti označovat. Například grafickou desetihodnotovou stupnicí v podobě starověkého magického tetraktysu. Ten symbolizuje součet 1+2+3+4=10. Obsahuje jeden velký trojúhelník a uvnitř devět malých. Plně vybarvený tetraktys by označoval úplnou pravdu na úrovni matematiky. Samotný velký trojúhelník potom nejnižší stupeň pravdivosti. Malé trojúhelníky by se přitom vybarvovaly zleva zezdola úměrně stupni pravdivosti.

Co je tedy pravda? Co nejvíce obarvený tetraktys. A lidská inteligence úsudku v případě nevybarvených trojúhelníků.